cse230

Bottling Computation Patterns

Another way to practice D.R.Y:

spot common computation patterns
refactor them into reusable higher-order functions (HOFs)
useful library HOFs: map, filter, and fold

EXERCISE: evens

Write a function evens that extracts only even elements from an integer list.

-- evens []        ==> []
-- evens [1,2,3,4] ==> [2,4]
evens       :: [Int] -> [Int]
evens []     = ... 
evens (x:xs) = ...

Example: four-letter words

Let’s write a function fourChars:

-- fourChars [] ==> []
-- fourChars ["i","must","do","work"] ==> ["must","work"]
fourChars :: [String] -> [String]
fourChars []     = ... 
fourChars (x:xs) = ...

Yikes, Most Code is the Same

Lets rename the functions to foo:

foo []            = []
foo (x:xs)
  | x mod 2 == 0  = x : foo xs
  | otherwise     =     foo xs

foo []            = []
foo (x:xs)
  | length x == 4 = x : foo xs
  | otherwise     =     foo xs

Only difference is the condition

x mod 2 == 0 vs length x == 4

Moral of the day

D.R.Y. Don’t Repeat Yourself!

Can we

reuse the general pattern and
substitute in the custom condition?

HOFs to the rescue!

General Pattern

expressed as a higher-order function
takes customizable operations as arguments

Specific Operation

passed in as an argument to the HOF

The “filter” pattern

General Pattern

HOF filter
Recursively traverse list and pick out elements that satisfy a predicate

Specific Operations

Predicates isEven and isFour

filter bottles the common pattern of selecting elements from a list that satisfy a condition:

Let’s talk about types

-- evens [1,2,3,4] ==> [2,4]
evens :: [Int] -> [Int]
evens xs = filter isEven xs
  where
    isEven :: Int -> Bool
    isEven x  =  x `mod` 2 == 0

filter :: ???

-- fourChars ["i","must","do","work"] ==> ["must","work"]
fourChars :: [String] -> [String]
fourChars xs = filter isFour xs
  where
    isFour :: String -> Bool
    isFour x  =  length x == 4

filter :: ???

So what’s the type of filter?

filter :: (Int -> Bool) -> [Int] -> [Int] -- ???

filter :: (String -> Bool) -> [String] -> [String] -- ???

It does not care what the list elements are
- as long as the predicate can handle them
It’s type is polymorphic (generic) in the type of list elements

-- For any type `a`
--   if you give me a predicate on `a`s
--   and a list of `a`s,
--   I'll give you back a list of `a`s 
filter :: (a -> Bool) -> [a] -> [a]

Example: all caps

Lets write a function shout:

-- shout []                    ==> []
-- shout ['h','e','l','l','o'] ==> ['H','E','L','L','O']

shout :: [Char] -> [Char]
shout []     = ...
shout (x:xs) = ...

Example: squares

Lets write a function squares:

-- squares []        ==> []
-- squares [1,2,3,4] ==> [1,4,9,16]

squares :: [Int] -> [Int]
squares []     = ...
squares (x:xs) = ...

Yikes, Most Code is the Same

Lets rename the functions to foo:

-- shout
foo []     = []
foo (x:xs) = toUpper x : foo xs

-- squares
foo []     = []
foo (x:xs) = (x * x)   : foo xs

Lets refactor into the common pattern

pattern = ...

The “map” pattern

General Pattern

HOF map
Apply a transformation f to each element of a list

Specific Operations

Transformations toUpper and \x -> x * x

map bottles the common pattern of iteratively applying a transformation to each element of a list:

EXERCISE: refactor with map

With map defined as:

map f []     = []
map f (x:xs) = f x : map f xs

refactor shout and squares to use map:

shout   xs = map ...

squares xs = map ...

The Case of the Missing Parameter

The following definitions of shout are equivalent:

shout :: [Char] -> [Char]
shout xs = map (\x -> toUpper x) xs

and

shout :: [Char] -> [Char]
shout = map toUpper

Where did xs and x go???

The Case of the Missing Parameter

Recall lambda calculus:

The expressions f and \x -> f x are in some sense “equivalent”

as long as x not in FV(f)

because they behave the same way when applied to any argument e:

(\x -> f x) e
=b> f e

Transforming \x -> f x into f is called eta contraction

and the reverse is called eta expansion

In Haskell we have:

shout xs = map (\x -> toUpper x) xs

is syntactic sugar for:

shout 
  =d> 
\xs -> map (\x -> toUpper x) xs
  =e> -- eta-contract outer lambda
map (\x -> toUpper x) xs
  =e> -- eta-contract inner lambda
map toUpper xs

More generally, whenever you want to define a function:

f x y z = e x y z

you can save some typing, and omit the parameters:

as long as x, y, and z are not free in e

f = e

QUIZ

What is the type of map?

map f []     = []
map f (x:xs) = f x : map f xs

(A) (Char -> Char) -> [Char] -> [Char]

(B) (Int -> Int) -> [Int] -> [Int]

(C) (a -> a) -> [a] -> [a]

(D) (a -> b) -> [a] -> [b]

(E) (a -> b) -> [c] -> [d]

The type of “map”

-- For any types `a` and `b`
--   if you give me a transformation from `a` to `b`
--   and a list of `a`s,
--   I'll give you back a list of `b`s 
map :: (a -> b) -> [a] -> [b]

Type says it all!

Can you think of a function that:

has this type
builds the output list not by applying the transformation to the input list?

Example: summing a list

-- sum []      ==> 0
-- sum [1,2,3] ==> 6
sum :: [Int] -> Int
sum []     = ...
sum (x:xs) = ...

Example: string concatenation

-- cat [] ==> ""
-- cat ["carne","asada","torta"] ==> "carneasadatorta"
cat :: [String] -> String
cat []     = ...
cat (x:xs) = ...

Can you spot the pattern?

-- sum
foo []     = 0
foo (x:xs) = x + foo xs

-- cat
foo []     = ""
foo (x:xs) = x ++ foo xs

pattern = ...

The “fold-right” pattern

foldr op base []     = base
foldr op base (x:xs) = op x (foldr op base xs)

General Pattern

Recurse on tail
Combine result with the head using some binary operation

foldr bottles the common pattern of combining/reducing a list into a single value:

EXERCISE: refactor with fold

With foldr defined as:

foldr op base []     = base
foldr op base (x:xs) = op x (foldr op base xs)

refactor sum and cat to use foldr:

sum xs = foldr op base xs
  where
    base     = ...
    op x acc = ...

cat xs = foldr op base xs
  where
    base     = ...
    op x acc = ...

Now use eta-contraction to make your code more concise!

Solution

sum xs = foldr op base xs
  where
    base     = 0
    op x acc = x + acc

cat xs = foldr op base xs
  where
    base     = ""
    op x acc = x ++ acc

or, more concisely:

sum = foldr (+) 0

cat = foldr (++) ""

Executing “foldr”

To develop some intuition about foldr lets “run” it by hand.

foldr op base []     = base
foldr op base (x:xs) = op x (foldr op base xs)

foldr op b (a1:a2:a3:[])
==> 
  a1 `op` (foldr op b (a2:a3:[]))
==> 
  a1 `op` (a2 `op` (foldr op b (a3:[])))
==> 
  a1 `op` (a2 `op` (a3 `op` (foldr op b [])))
==> 
  a1 `op` (a2 `op` (a3 `op` b))

Look how it mirrors the structure of lists!

(:) is replaced by op
[] is replaced by base

For example:

foldr (+) 0 [1, 2, 3, 4]
  ==> 1 + (foldr (+) 0 [2, 3, 4])
  ==> 1 + (2 + (foldr (+) 0 [3, 4]))
  ==> 1 + (2 + (3 + (foldr (+) 0 [4])))
  ==> 1 + (2 + (3 + (4 + (foldr (+) 0 []))))
  ==> 1 + (2 + (3 + (4 + 0)))

Accumulate the values from the right!

QUIZ

What is the most general type of foldr?

foldr op base []     = base
foldr op base (x:xs) = op x (foldr op base xs)

(A) (a -> a -> a) -> a -> [a] -> a

(B) (a -> a -> b) -> a -> [a] -> b

(C) (a -> b -> a) -> b -> [a] -> b

(D) (a -> b -> b) -> b -> [a] -> b

(E) (b -> a -> b) -> b -> [a] -> b

Answer: D

QUIZ

Recall the function to compute the len of a list

len :: [a] -> Int
len []     = 0
len (x:xs) = 1 + len xs

Which of these is a valid implementation of len

A. len = foldr (\n -> n + 1) 0

B. len = foldr (\n m -> n + m) 0

C. len = foldr (\_ n -> n + 1) 0

D. len = foldr (\x xs -> 1 + len xs) 0

E. All of the above

HINT: remember that foldr :: (a -> b -> b) -> b -> [a] -> b!

The Missing Parameter Revisited

We wrote foldr as

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr op base []     = base
foldr op base (x:xs) = op x (foldr op base xs)

but can also write this

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr op base  = go 
  where
     go []     = base
     go (x:xs) = op x (go xs)

Can someone explain where the xs went missing ?

Aside: folding right vs left

We can also fold a list from the left:

foldl op b (a1:a2:a3:[])
==>
  foldl op (b `op` a1) (a2:a3:[])
==>
  foldl op ((b `op` a1) `op` a2) (a3:[])
==>
  foldl op (((b `op` a1) `op` a2) `op` a3) []
==>
  ((b `op` a1) `op` a2) `op` a3

Contrast this to folding from the right:

foldr op b (a1:a2:a3:[])
==> 
  a1 `op` (foldr op b (a2:a3:[]))
==>
  a1 `op` (a2 `op` (foldr op b (a3:[])))
==>
  a1 `op` (a2 `op` (a3 `op` (foldr op b [])))
==>
  a1 `op` (a2 `op` (a3 `op` b))

Left vs. Right

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr op base  = go 
  where
     go []     = base
     go (x:xs) = op x (go xs)

foldl :: (b -> a -> b) -> b -> [a] -> b -- Different type!
foldl op base  = go base
  where
     go acc []     = acc
     go acc (x:xs) = go (op acc x) xs -- Different recursion!

Trees

Recall binary trees of integers ITree from last time.

They can be generalized to trees of any type a:

data Tree a 
  = Leaf 
  | Node a (Tree a) (Tree a)

t1234 :: Tree Int
t1234 = Node 1 
          (Node 2 (Node 3 Leaf Leaf) Leaf) 
          (Node 4 Leaf Leaf)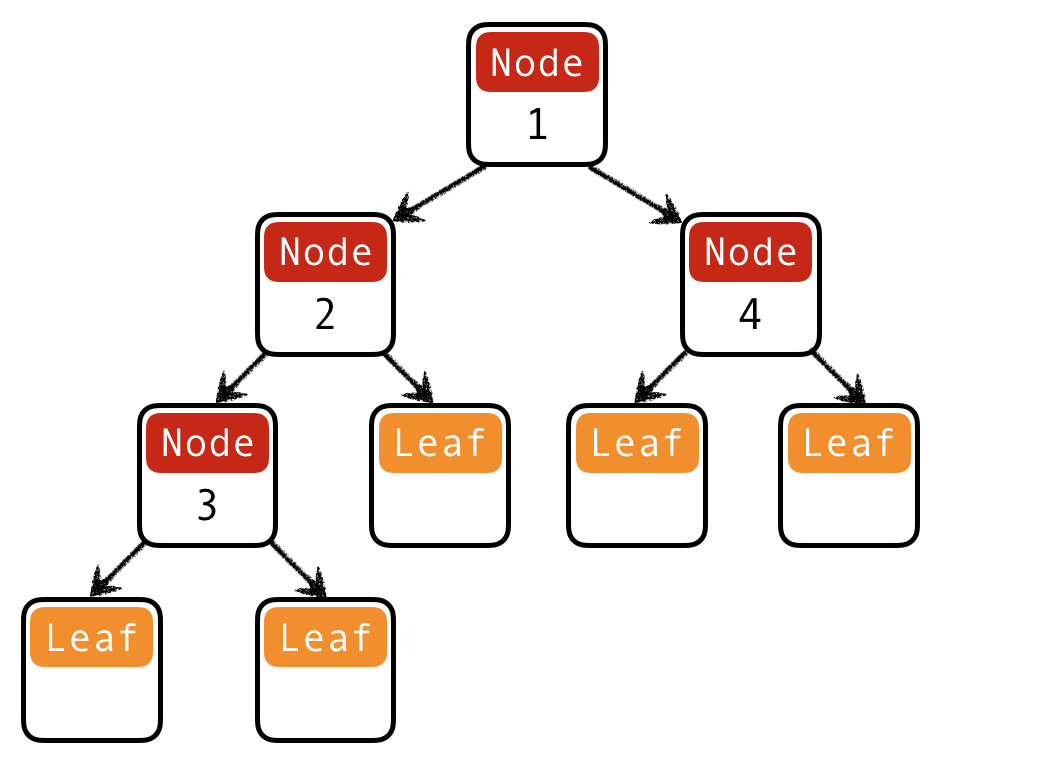

EXERCISE: tree height

Write a function to compute the height of a tree, where

height is the max number of Nodes on a path from the root to a leaf

data Tree a = Leaf | Node a (Tree a) (Tree a)

height :: Tree a -> Int
height Leaf         = ???
height (Node x l r) = ???

>>> height t1234
3

Examples: tree sum

Let’s write a function to sum the leaves of an Int tree:

sumTree :: Tree Int -> Int
sumTree Leaf         = ???
sumTree (Node x l r) = ???

>>> sumTree t1234
10

Let’s write a function to gather all the elements in the tree:

toList :: Tree a -> [a] 
toList Leaf         = ??? 
toList (Node x l r) = ???

>>> toList t1234
[1,2,3,4]

Pattern: Tree Fold

Can you spot the pattern? Those three functions are almost the same!

Step 1: Rename to maximize similarity

-- height
foo Leaf         = 0
foo (Node x l r) = 1 + max (foo l) (foo l)

-- sumTree
foo Leaf         = 0
foo (Node x l r) = foo l + foo r

-- toList
foo Leaf         = []
foo (Node x l r) = x : foo l ++ foo r

Step 2: Identify the differences

Step 3 Make differences a parameter

foo p1 p2 Leaf         = ???
foo p1 p2 (Node x l r) = ???

Pattern: Tree fold

tFold op base Leaf         = base 
tFold op base (Node x l r) = op x (tFold op base l) (tFold op base r)

Lets try to work out the type of tFold!

tFold :: ??? -> ??? -> Tree a -> ???

tFold :: (a -> b -> b -> b) -> b -> Tree a -> b
tFold op base = go
  where
    go Leaf         = base
    go (Node x l r) = op x (go l) (go r)

QUIZ

Suppose that t :: Tree Int.

What does tFold (\x y z -> y + z) 1 t return?

a. 0

b. the largest element in the tree t

c. the number of nodes of the tree t

d. the number of leaves of the tree t

e. type error

EXERCISE: using tree fold

Write a function to compute the largest element in a tree or 0 if tree is empty or all negative.

treeMax :: Tree Int -> Int
treeMax t = tFold f b t 
  where 
     b       = ???
     f x l r = ???

Recall that tFold is defined as

tFold :: (a -> b -> b -> b) -> b -> Tree a -> b
tFold op base = go
  where
    go Leaf         = base
    go (Node x l r) = op x (go l) (go r)

Map over Trees

We can also write a tmap equivalent of map for Trees

treeMap :: (a -> b) -> Tree a -> Tree b
treeMap f Leaf       = Leaf
treeMap f (Node x l r) = Node (f x) (treeMap f l) (treeMap f r)

which gives

>>> treeMap (\n -> n * n) tree1234     -- square all elements of tree
Node 1 (Node 4 (Node 9 Leaf Leaf) Leaf) (Node 16 Leaf Leaf)

EXERCISE: map via fold

Can we rewrite treeMap using tFold?

treeMap :: (a -> b) -> Tree a -> Tree b
treeMap f = tFold op base 
  where 
     base     = ??? 
     op x l r = ???

Folding custom data types

We can also write fancy folds for our own data types!

For example, here is a “directory” data type from HW1:

data Dir a 
  = Fil a          -- A single file named `a`
  | Sub a [Dir a]  -- A sub-directory name `a` with contents `[Dir a]`

data DirElem a 
  = File a         -- A single File named `a` 
  | SubDir a       -- A single Sub-Directory named `a`

foldDir :: ([a] -> r -> DirElem a -> r) -> r -> Dir a -> r
foldDir op r0 dir = go [] r0 dir  
  where
      go path r (Fil a)    = op path r (File a)  
      go path r (Sub a ds) = foldl' (go path') r' ds                          
        where 
            r'    = op path r (SubDir a)  
            path' = a:path

foldDir takes as input

an operation op of type [a] -> r -> DirElem a -> r
- takes as input the path [a] , the current result r, the next DirElem [a]
- and returns as output the new result r
an initial value of the result r0 and
directory to fold over dir

And returns the result of running the accumulator over the whole dir.

Higher Order Functions

Iteration patterns over collections:

Filter values in a collection given a predicate
Map (iterate) a given transformation over a collection
Fold (reduce) a collection into a value, given a binary operation to combine results

HOFs can be put into libraries to enable modularity

Data structure library implements map, filter, fold for its collections
- generic efficient implementation
- generic optimizations: map f (map g xs) --> map (f.g) xs
Data structure clients use HOFs with specific operations
- no need to know the implementation of the collection
- less to write
- easier to communicate
- avoid bugs due to repetition

Indeed, HOFs were the basis of map/reduce and the big-data revolution

Can parallelize and distribute computation patterns just once
Reuse across hundreds or thousands of instances!